2048
"Вы уже устали терять время в установлении рекордов в этой игре? Тогда я попробую помочь Вам :)

Я больше четырех месяцев пытался хаотично собрать "2048" в одной клеточке в этой игре. Я собирал все возможные сочетания рядом, пытался все держать в центре поля, строить горизонтальные линии не взирая на "номинал" кубиков... Но достичь рекордов можно только так:
При любых системах хаотичных собирания максимум, что я достиг - это расположенные по разным сторонам игрового поля два кубика по "1024", которые я так и не смог слить воедино в желанную "2048". Достичь успеха можно только в случае собирания кубиков в каком-либо из углов игрового поля и выстраивания кубиков в виде змейки со строгим соблюдением номинала, как это показано на картинке вверху. После принятия такой стратегии я собирал "2048" в 4 случаях из 5. "4096" или даже два по "4096" - примерно в 1 случае из 4...


Главной проблемой стало то, что рано или поздно строящаяся змейка может быть убита появлением такой вот "китайской стены":

Тут ничего другого не остается, как сдвигать ее в право, что приведет к обязательному внедрению следующей выпавшей "2" или "4" ближе к голове змеи. И чем дольше играешь, тем больше вероятность появления такой ситуации и, соответственно, увеличения потраченного впустую времени в случае игры в режиме, где нельзя сделать отмену хода... В таком режиме я пытался сложить "8192" около 1.5 месяцев. Максимум, чего смог добиться: один раз собрал два кубика по "4096" на одной линии игрового поля, которые не успел соединить... И когда мне все-таки удалось сложить "8192", то к невероятному, как я считаю, везению примешалась горечь от того, что забыл сделать скриншоты этого события. Поэтому повторение этого достижения и движение дальше по лестнице рекордов делал уже в режиме, где можно отменять 10 последних ходов:

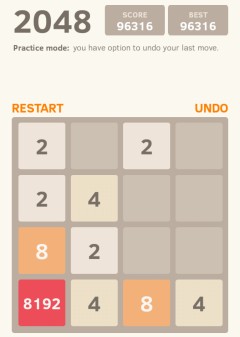
Глупо рассчитывать на такую удачу, что бы собрать даже "8192", не то что бы пойти дальше к "16384"...
Теоретический максимум данной игры составляет 2, возведенное в степень, равную количеству ячеек на игровом поле. 2^16 = 65536. Этот придел обусловлен тем, что не получится построить змейку, отличную от последовательности 2,4,8,16....32768, из которой можно собрать только 65536.


Но так как игра предусматривает случайное выпадение не "2", а "4", то в случае отмены последних ходов появляется возможность дожидаться выпадения в конце змейки двух "4". Это позволяет выстроить змейку 4,8,16,32...65536, что позволяет собрать 2^17 = 131072!


И теперь это уже предел - на игровом поле 4x4 большее число уже не собрать, только если там не будут появляться "8" :)
Соответственно для поля 5x5 предел составляет 2^26 = 67 108 864. Виденные мной варианты с полем 7x7 даже считать не буду...
Удачи Вам в достижении новых рекордов :)"
| Прикрепленный файл | Размер |
|---|---|
| 2048_131072+after.jpg | 18.63 Кбайт |
| 2048_131072+before.jpg | 17.21 Кбайт |
| 2048_65536+after.jpg | 12.8 Кбайт |
| 2048_65536+before.jpg | 17.08 Кбайт |
| 2048_8192+after.jpg | 13.01 Кбайт |
| 2048_4096+before.jpg | 12.62 Кбайт |
| 2048_2048+block.jpg | 14.96 Кбайт |
| 2048_8192+before.jpg | 15.91 Кбайт |
| 2048_4096+after.jpg | 13.13 Кбайт |


Отправить новый комментарий